初めての機械学習【分類と回帰】について（教師あり学習の場合を例に）

機械学習の勉強を始めて、いろいろな専門用語に出会うと思ういます。その中の一つに「回帰」という言葉があります。この文字からはなかなか内容が推測できず、戸惑う方がおられるのではないでしょうか。今回は教師あり学習に例にとり、その大きな２つのタイプである分類と回帰、特に回帰の意味について少し掘り下げてお話ししていきたいと思います。

分類と回帰の違いと定義

それでは、まずは理解しやすい「分類(Classification)」の方からお話を始めたいと思います。最も単純は分類の例は与えられたデーターから「Yes」または「No」を判断するもの(binary classification)です。実際の身近な例としてはメールを有害なスパムメールか無害の一般メールかを識別するスパムメールフィルターです。
また、それ以外の分類の例を挙げれば、ユリの種類を花の花弁や萼片のサイズで２つを超える種類に分類するものです(Multiclass clacification)。これに関しては、K近傍法を使っての実際のPythonでの実装をぼくの別の記事で説明していますので、興味のある方は、以下のリンクから参照してみて下さい。

LINK：【初めての機械学習】PythonとScikit-Learnを使ってK近傍法を実装

大雑把な言い方をすると、分類（Classidication)とは、Inputをもとに断続的なOutputを予測（Predict)するのです。
それでは、回帰（Regression)とはなんでしょうか。回帰という日本語も意味を掴みにくい言葉ですが、英語の「Regression」も日本人にとって馴染みが薄く意味のつかみにくい単語のように思います。
ここでも大雑把な言い方をすれば、回帰（Regression)とはInputをもとに連続的なOutputを予測（Predict)するものです。つまり、値段や面積、時間、など数値で表されるものです。断続的、連続的との定義づけは、「Yes」や「No」、男性と女性、TruthとFailの間に中間的な値が無いのに対して、1と2の間には、1.1, 1.12と中間的な値を取れることによって判断できるかと思います。
それでは、まず実際に簡単な回帰の実装をPythonとsklearnを使って行ってみましょう。

回帰の実装の準備

それでは、まずは回帰の実装に適したデータセットをダウンロードしましょう。ここでは、sklearnのトイデータセットのうち、回帰に適した「ボストン市の住宅価格データ(Boston house prices dataset)」をダウンロードします。ダウンロードのためのコードは以下の通りです。

このトイデータセットにはdataとして、506地域の13項目の価、targetとしてその地区の住宅の中央値（1000ドル単位）が収められています。以下に13項目の構成を示します。

それでは上記の１３項目と地区の住宅価格の中央値との関係を散布図で見てみましょう。散布図の表示に必要なコードは以下の通りです。また、散布図表示のためのコードにつき、以下のぼくの別記事で説明しています。わからないとこらがあれば、参照してください。

LINK：【Jupyter Notobook】Matplotlibを使って２次元グラフを描こう

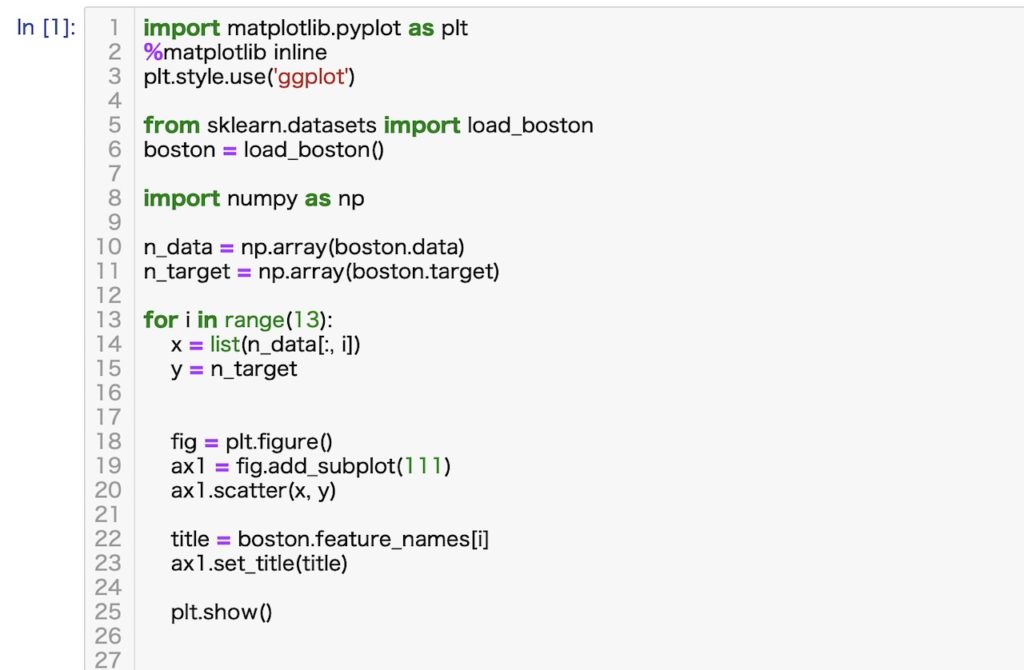
上記のコードにより出力された散布図を以下に示します。

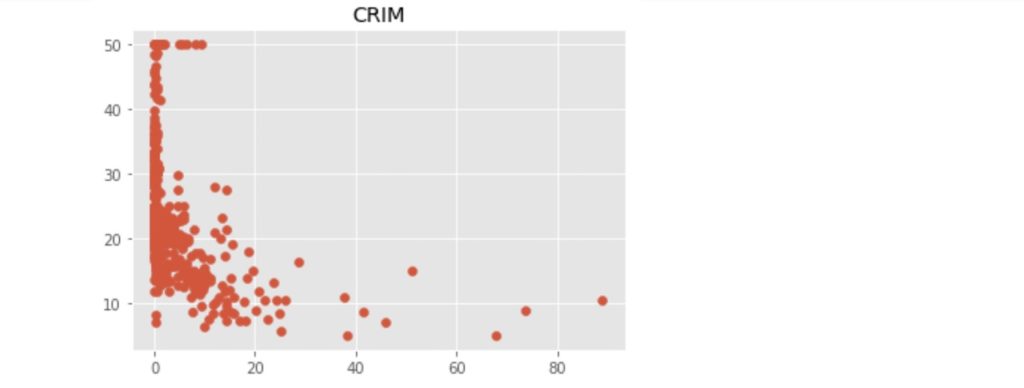
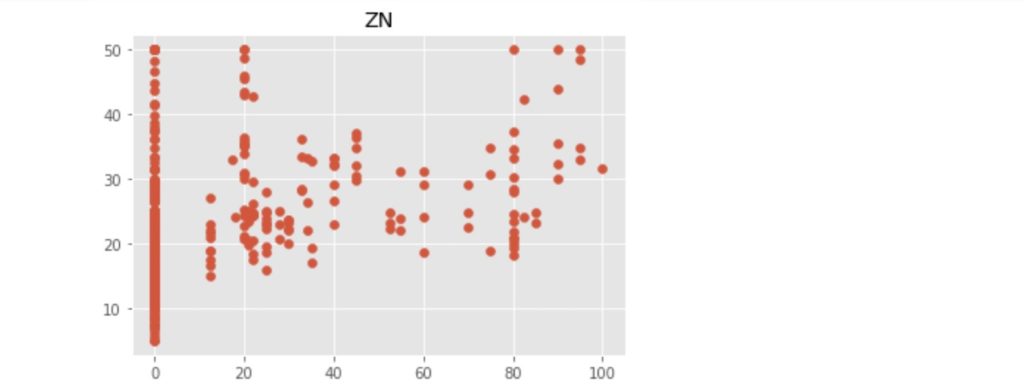
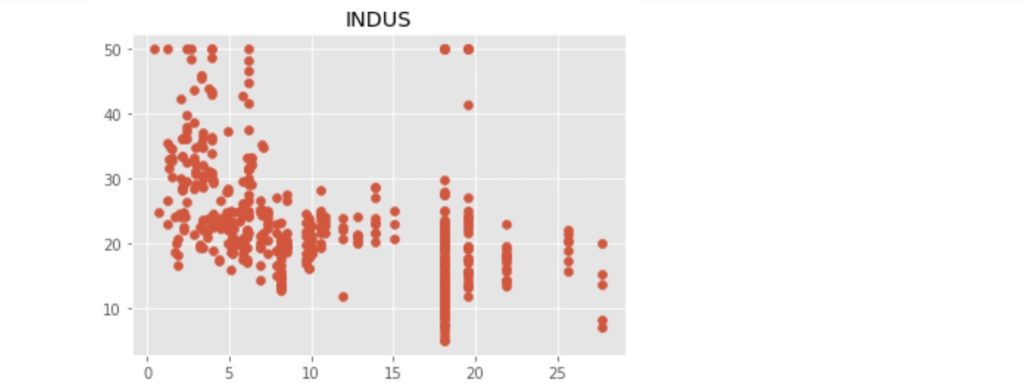
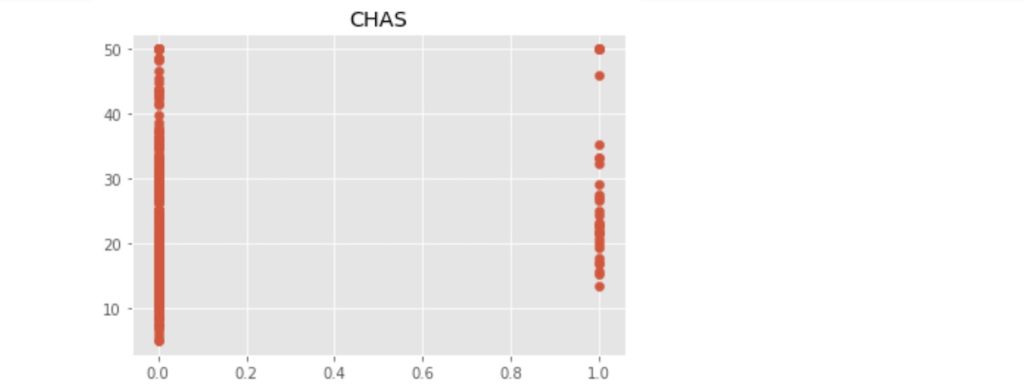
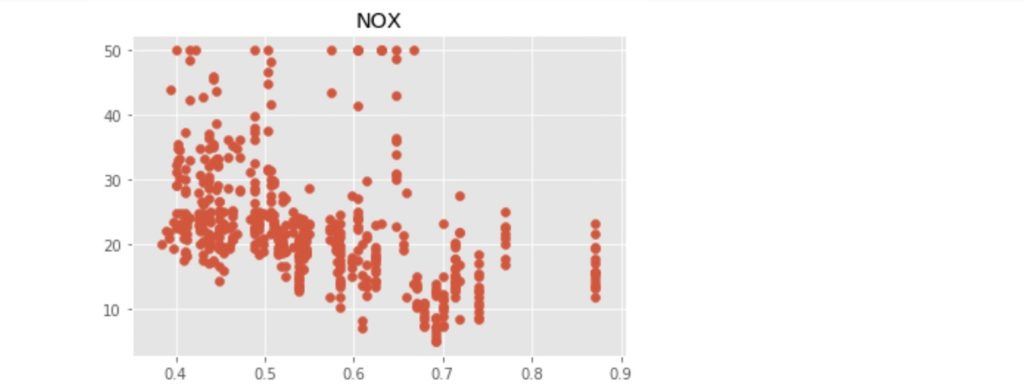
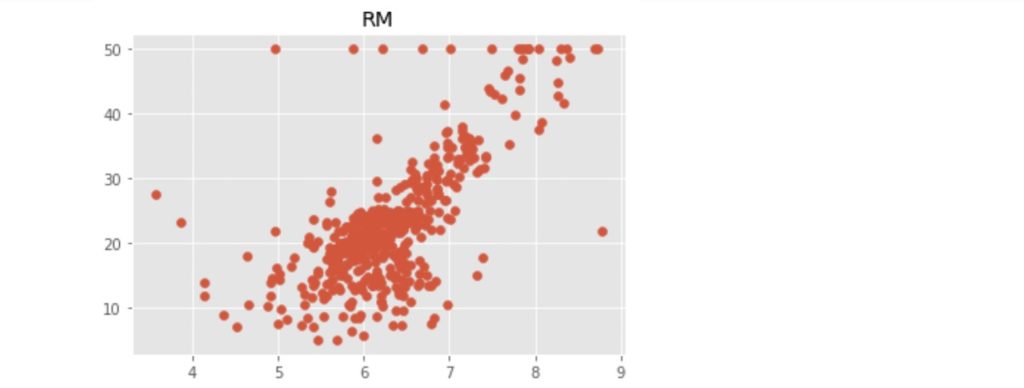
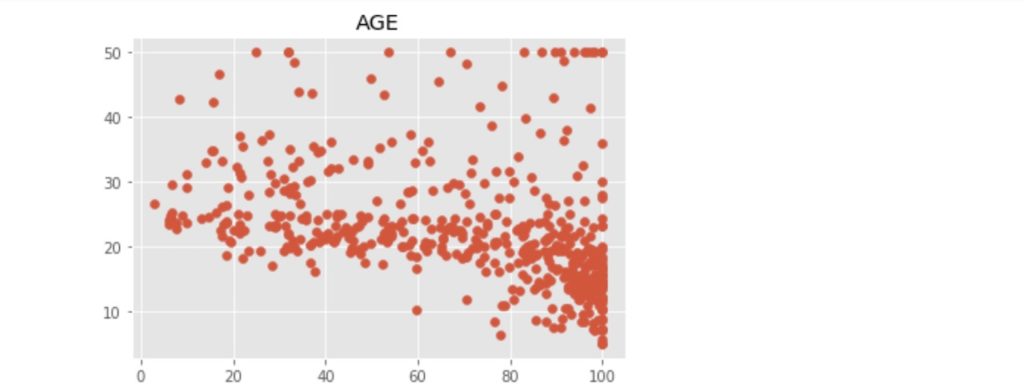
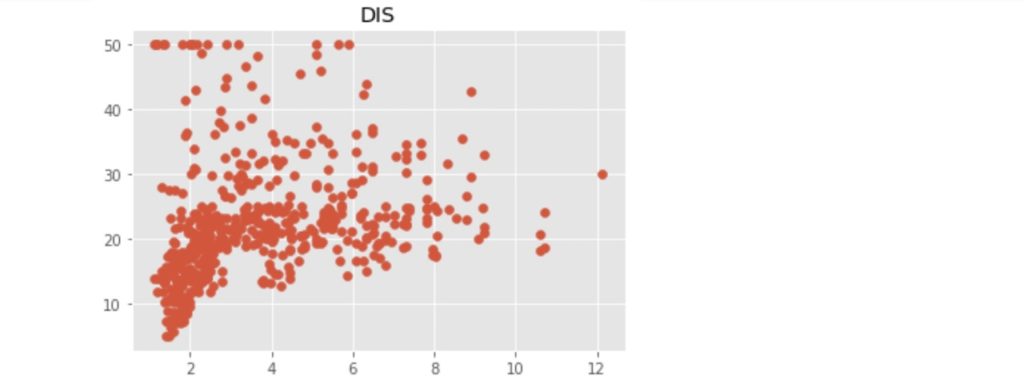
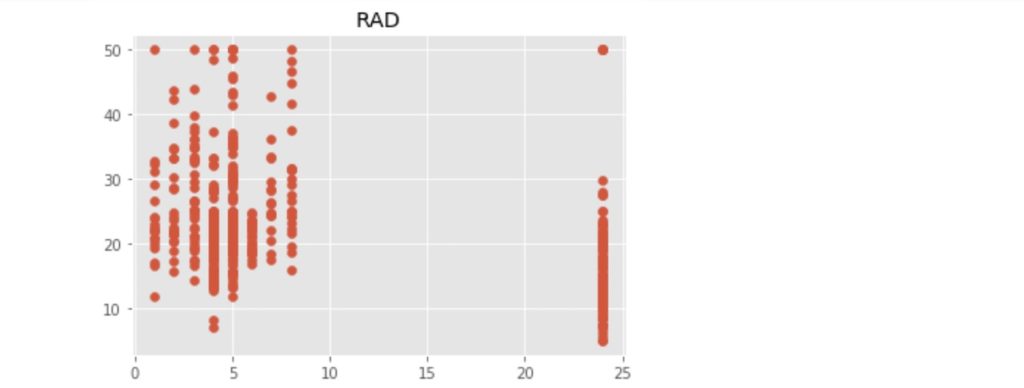
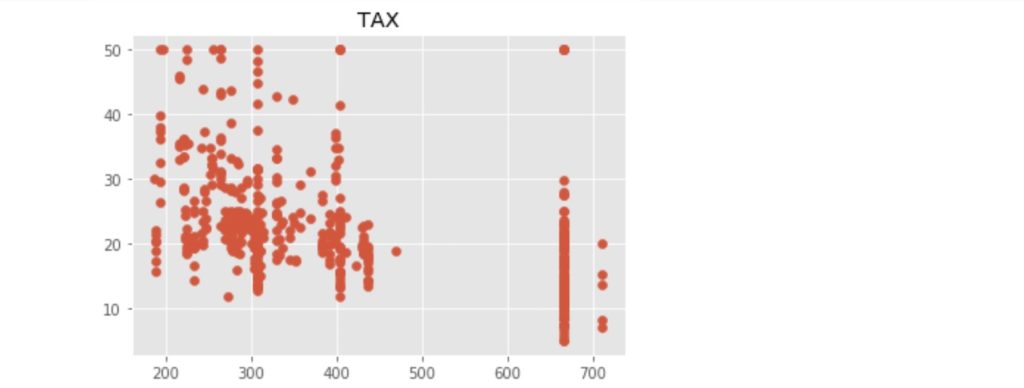
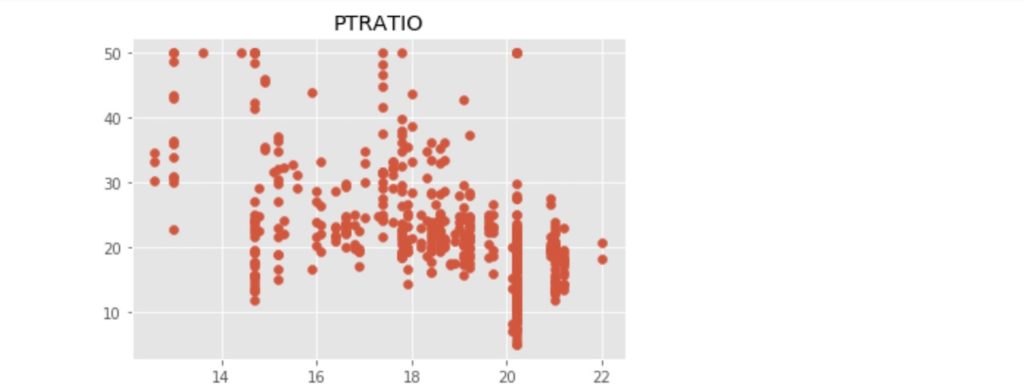
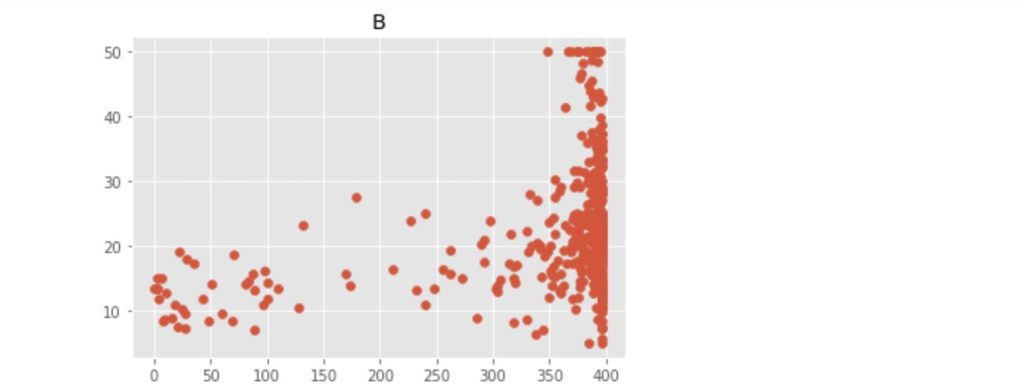
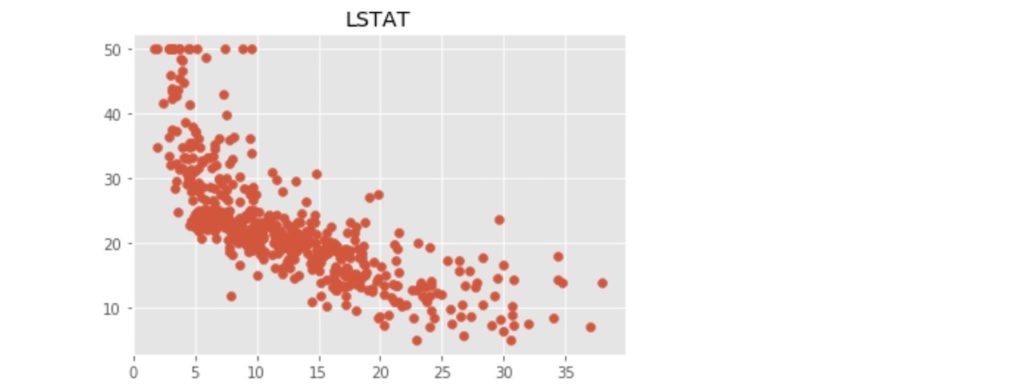
この中で、「RM」：住宅の平均部屋数と「LSTAT」：給与の低い職業に従事する人の割合（％）が価格の中心値と比較的明らかに相対関係にあるようです。ここでは、「LSTAT」を使って、N近傍法（kNN）での回帰をn値が1, 3, 5 ... 21の場合で行い、それぞれの評価まで行いたいと思います。

N近傍法による回帰の実装

上記のコードが実装のためのすべてのコードです。Pythonでは機械学習のためのライブラリーが豊富に準備されているため、驚くほど簡単なコードで機械学習の実装を行うことができます。
それでは、簡単に上記のコードを説明します。

ライン１から６までは、ライブラリーの読み込み、
ライン９と11はデータセットをそれぞれの変数に読み込んでいます。
ライン13と15で、データーセットから「LSTAT」のデータを選択して、入力データ「X」とその回答「y」を作っています。
ライン18でX, yを学習データとテストデータに分離しています。（デフォルトでは学習データ：テストデータ＝３：１に分離されます。）
ライン20では、回帰用のN近傍法のアルゴリズムを読み込んでいます。
ライン22では、読み込んだアルゴリズムを学習データをもとに学習しています。（N近傍法では、他のアルゴリズムと学習の意味が少し違うのですが、ここでは無視します。）

それでは実際にこのコードを使って、地区の住居価格の中央値を推測してみましょう。今回は、
LSTAT：給与の低い職業に従事する人の割合（％）のみに着目していますから、この値から価格の中央値を推測することになります。例えば、LSTATのパーセントが5％から35％までを5％区切りで推測した場合を出力させるコードとその結果は以下のようになります。

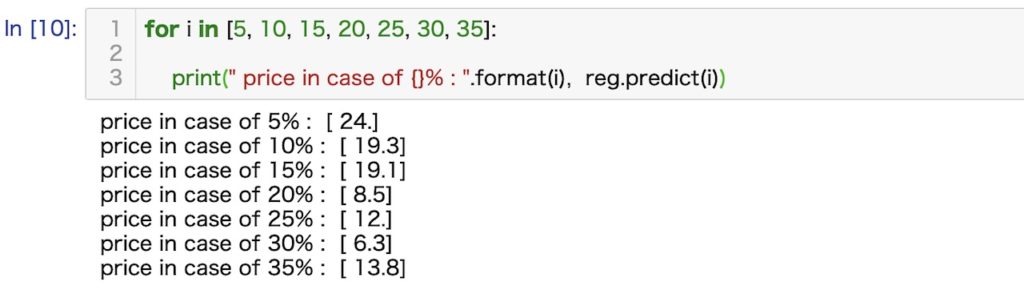
また、上記の結果をグラフ上に示す（青丸）と以下のようになります。

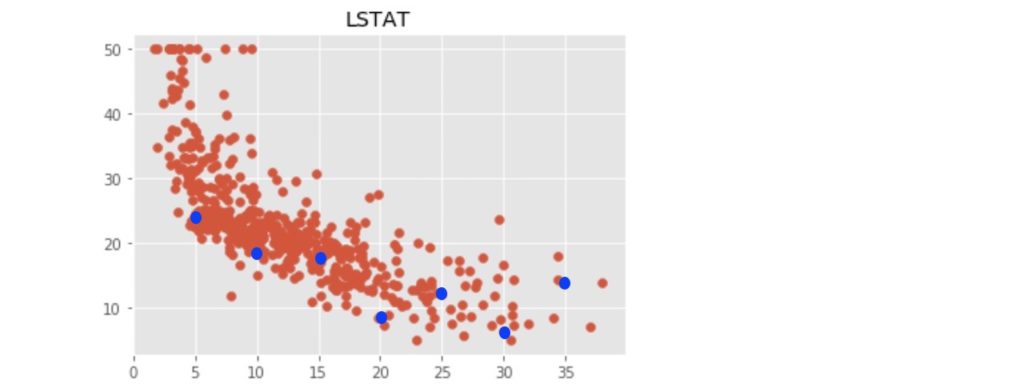
評価方法について

回帰モデルの結果の評価指数には、平均絶対誤差（MAE)、平均二乗誤差（MSE)、二乗平均平方根誤差（RMSE)、決定係数（R²)がありますが、ここでは決定係数（寄与率とも呼びます）を使います。詳しい計算方法はここでは省きますが、理想的な完璧な推測を行った場合はこの決定係数は１、本来の解答の平均値を推測の結果とした場合には、この値は０になります。また、それよりも結果が悪い場合はマイナスの値をとる場合もあります。

上記のコードで決定係数（R²)を表示できるのですが、その結果は控えめに見てもよろしくない結果です。これは比較的相関関係が出ている要素を選んだと言っても１３個のうちの１つに着目しているに過ぎないこと、また、N近傍法でN=1つまり、１番近いサンプルの数値を参照しているに過ぎないからです。N=3とすると、１番近いサンプル、２番目に近いサンプル、３番目に近いサンプルの平均値を参照します。
それでは、Nの値を３、５、７と２１まで変化させた時の定係数（R²)の変化をグラフ上で見てみましょう。

上記のグラフから、N=13の時に定係数（R²)の値はもっとも高くなっていることがわかります。

まとめ

いかがでしたでしょうか。実装を等して、回帰モデルのイメージを掴んでいただけたでしょうか。
また、単純とは言え、機械学習の実装がこれほど簡単に行えることに驚かれたのではないでしょうか。これは充実したライブラリーを持っているPythonならではの強みと言えます。
それでは、最後までお付き合い頂き、ありがとうございました。さようなら。